Technical Articles and Product Descriptions

Reference Materials

Additional Products

Race Engine Technology Magazine

This page presents the detailed, factual data (with pictures) which demonstrate that the ProDrive toothbelt system applies a substantially greater load to the secondary shaft than does either the factory chain drive or the Behuncik belt drive.

Despite the publication of this information in mid-2003, and despite a clear presentation of these data at Homer's-2004, ProDrive apparently thinks that if they continue to deny these facts, they will just go away. Well, not quite yet.

There are three reasons that the ProDrive system applies substantially greater bending load to the secondary shaft, which will be explained in detail below.

HERE IS THE SUMMARY.

1. SMALLER SPROCKET DIAMETER

The ProDrive secondary sprocket is smaller in diameter than either the chain drive sprocket or the Behuncik sprocket, which generates a LARGER drive tension for the same applied torque;

2. LARGER BENDING MOMENT

The ProDrive secondary sprocket applies the drive tension HIGHER on the secondary shaft than the factory chain, regardless of how many times ProDrive denies it (see detailed proof below). That produces a larger bending moment for the same applied belt / chain force.

3. PRELOAD

ALL belt systems require PRELOAD in order to transmit power. Regardless of ProDrive's claims, if the belt can transmit the power to the main rotor, then either:

1. the belt has at least the required preload, OR
2. the belt is generating a LARGER preload than it would if it were properly tensioned (making it worse than shown here). This is the phenomenon known as "self-tensioning", explained in the section on Gates Toothbelt Issues.

When you combine the effects of these three factors, you find that a ProDrive belt system, properly tensioned for cruise power, applies a 33.3% larger bending stress to the secondary shaft, which results in a 33.3% larger deflection, which leads to a faster fretting rate and a higher fatigue stress. AND, that bigger fatigue stress is being applied to the shaft at ALL POWER SETTINGS.

HERE ARE THE DETAILS.

1.   SMALLER SPROCKET DIAMETER

Everyone who has used a torque wrench will understand that if you use a wrench with a 2-foot-long handle to apply 100 lb-ft of torque to a bolt, you will be pulling on the wrench handle with a force of 50 pounds. If you decide to use a wrench with a 1.5-foot-long handle, you must pull on the wrench with a 67 pound force to get the same 100 lb-ft of torque.

The same principle applies to the drive sprocket diameter. With a chain drive or belt drive or gear drive, the force transmitted by the chain or belt or gear is the applied torque times half the pitch diameter.

If the secondary shaft is applying 95 HP to the main rotor, the torque is 230 lb-ft or 2760 lb.-in. (230 x 12)

CHAIN DRIVE: Morse Chain (a leading manufacturer of 50-series roller chain) lists the pitch diameter of the 19-tooth, 50-series sprocket as 3.797 inches. Therefore, the driving tension applied to the chain by that 2760 lb.-in. of torque is:

Chain Force = torque / (1/2 sprocket pitch diameter)
Chain Force = 2760 / (1/2 * 3.797) = 1454 pounds.

PRODRIVE BELT: We have measured several ProDrive sprockets, and the outside diameter is the same as Gates published dimension of 3.349 inches, and on that basis, we use the Gates figure of 3.409 inches for the pitch diameter for that sprocket.

Therefore, for the same 95 HP applied to the main rotor (2762 lb-in of torque), the driving tension is:

Belt Force = torque / (1/2 sprocket outside diameter)
Belt Force = 2760 / (1/2 * 3.409) = 1619 pounds.

No matter how you slice it, 1619 is 11.4% greater than 1454. That means if the same torque is applied to each system, the bending force applied by the ProDrive system will be 11.4% greater than the chain BY VIRTUE OF THE SPROCKET DIAMETER ALONE, without taking preload into account.

2.   LARGER BENDING MOMENT

The ProDrive sprocket is almost 3/4" taller than the chain sprocket, and, although it sits slightly lower on the shaft than the chain sprocket, the substantially greater height causes the ProDrive system to apply a larger bending moment to the shaft for the same applied force.

Here is how we determined the comparative bending moment arm values.

(a) CHAIN DRIVE MOMENT ARM

This picture shows a side view of a 35mm secondary with the chain drive sprocket installed. The vertical location of the sprocket is set by the 3-hole plate which bolts to the end of the shaft and to the top of the sprocket.

We measured the 1.910 height dimension on a factory sprocket. The 2.520 dimension is from the top of the sprocket to the upper edge of the bearing. The chain load can be assumed to be applied at the vertical midpoint of the sprocket.

The point of maximum bending moment (substantiated by our FEA studies) is roughly in the middle of the spherical bearing. The bearing thickness is 0.906. 

Using simple arithmetic and those facts alone, the moment arm of the Chain Drive sprocket is

2.520 + 1/2 ( 0.906) - 1/2 (1.910) = 2.018

(b) PRODRIVE MOMENT ARM

ProDrive has claimed, both verbally and on their website, that the "bigger moment" argument is not significant because, they claim, their sprocket is installed much lower on the shaft than the chain sprocket, minimizing this effect. (They further claim that anyone knowledgeable about RotorWay helicopters will be aware of that "fact".)

Well folks, here's a photo taken of a RotorWay 162 in Homer's hangar. (Incidentally, this ship was having a re-install of a ProDrive system after the belt broke in half.)

We measured the distance from the bottom of the sprocket to the upper flat face of the bearing housing (where the taper ends) and found it to be 0.390 inches.

Based on that measurement (which should be fairly representative, and certainly correct since Homer was doing the install) we determined the effective moment arm of the ProDrive system, as follows.

Here's the side view of the 35mm secondary with a ProDrive sprocket installed at the height shown in the picture above, using the dimension we measured at Homer's. We measured the 2.625 height dimension on a ProDrive sprocket. The 3.087 dimension is from the top of the sprocket to the upper edge of the bearing. The bearing thickness is 0.906.

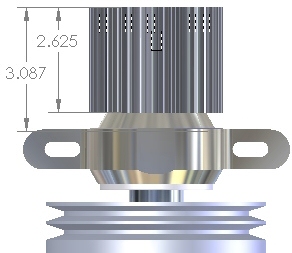Just as with the chain, the belt load can be assumed to be applied at the vertical midpoint of the sprocket. Using simple arithmetic and those facts alone, the moment arm of the ProDrive sprocket is:

3.087 + 1/2 ( 0.906) - 1/2 (2.625) = 2.227

No matter how you slice it, 2.227 is 10.4% greater than 2.018. That means if the same belt / chain load is applied to each system, the bending moment on the ProDrive system will be 10.4% greater BY VIRTUE OF THE SPROCKET HEIGHT ALONE, not accounting for preload and diameter effects.

NOTE that if we used ProDrive's method of calculating the moment arm, the increase produced by their system IS WORSE than shown here.

3.   PRELOAD

In order to present the ProDrive belt in the most favorable way, we will use a main rotor power value of 95 hp, fairly typical of a cruise value. (Using the max power value of 115 to 120 HP just makes the belt drive case worse.) As shown elsewhere on this site, 95 HP at the secondary RPM of 2168 is about 230 lb.-ft. of torque, or 2760 lb.-in.

In the ProDrive system (details), 2760 lb.-in. of torque produces a drive tension of 1620 pounds. At a 10:1 tension ratio with that driving tension, the loose span tension is 180 pounds (1620 / 9 ), and the tight side tension is 1800 pounds (1620 pounds driving tension plus 180 pounds loose side tension) for a total of 1980 pounds. (If you don't understand that, PLEASE look here.)

In the factory chain drive (details), there is no preload after a short amount of running time. However, the chain drive, transmitting the same 95 HP, has a loose span tension of 92 pounds, caused by the centrifugal force of the chain. The tight span tension is 1547 pounds (1455 pounds driving tension plus 92 pounds loose span tension) for a total of 1639 pounds.

4.   COMBINED EFFECT

In order to examine the combined effect of these three factors, you compare the total bending moment applied to the secondary by the chain and belt drives respectively.

When you multiply the bigger load applied to the shaft (the result of (1) the smaller sprocket and (2) the belt preload, as explained in 3. above) by the greater moment arm (resulting from the taller belt sprocket, as explained in B. above) you get an applied bending moment of 4409 lb.-in. for the belt drive.

The same calculation produces a bending moment of 3307 lb.-in. for the chain drive.

No matter how you slice it, that is a 33.3% larger bending moment applied by the ProDrive belt system, assuming the belt drive is tensioned correctly for AT LEAST the nominal cruise power (95 HP).

The numbers get worse if you assume the belt drive is correctly preloaded for the max main rotor power of around 120 HP.

Now, you must also consider the fact that ProDrive belt system is applying the same fatigue cycling load to the secondary shaft, whether it is idling or cruising. That fact alone contributes to the faster fretting, but when you add in the substantially bigger bending loads, the increased fatigue loading becomes very apparent.

Bottom line: We think the detailed analysis shows that the factory 35-mm system is not adequate, either in material or in design, to survive the extra deflection and fatigue loading imposed by the Pro-Drive™ belt system.

If you are using that drive system, it is up to you, the builder / operator, to apply whatever corrective measures you deem appropriate.