- Main V-belt Drive -
Power Transmission Properties
NOTE: All our Products, Designs, and Services are SUSTAINABLE, ORGANIC, GLUTEN-FREE, CONTAIN NO GMO's, and will not upset anyone's precious FEELINGS or delicate SENSIBILITIES
Before starting this section, it might be helpful to review the section dedicated to explaining the general characteristics of All Belt Drives.
Specifics of the RotorWay Main V-belt Drive
The RotorWay main power transmission mechanism from the engine to the secondary shaft is by means of eight "3V" section V-belts (3V-630), with each pair banded together into belted sets. The bands across the backs of the belts serve a very important function: they keep the belts from flipping over in the grooves in torsionally active systems.
The belts EPI examined were Bando brand. This is an offshore-sourced product which some experts in the power transmission business believe to be of less quality than the well-known domestics. HOWEVER, experience tends to indicate that these belts last quite well in service, which is unquestionably severe.
BELT LOADS
From the defined Max Power analysis parameters of 150 engine HP at 4250 RPM (185 lb-ft of mean torque) and the physical dimensions shown in the sketch above, the relevant belt load numbers can be calculated.
The sketch below is scaled to the sizes of the system components. The arc of contact on the driving pulley is about 149°. The belt velocity at 4250 RPM is about 6950 feet per minute. The calculated design tension ratio for 185 lb-ft of torque at 6950 fpm with a minimum arc of contact of 149°, is 3.75.
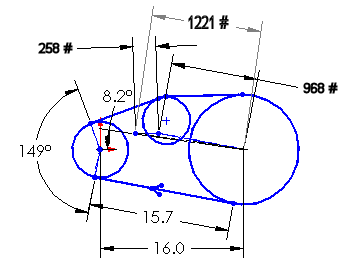
V-belt Drive at Max Power
The belt preload is determined from the maximum torque the system must transmit. At at 185 lb-ft of torque, the driving tension produced by the 6.25" diameter driving pulley is 710 pounds (185 x 12 / (6.25 / 2)). With the design tension ratio of 3.75, the calculated slack-side tension is 258 lbs. (710 / 2.75) and the tight side tension is 968 lbs. (710 + 258). That results in a required preload of 1226 lbs. (968 + 258) and the required tension ratio of 3.75 (968 / 258).
The dotted lines in the sketch emanating from the center of the large pulley are scaled representations of the tight and slack side tension vectors at 185 lb-ft of torque (968 lbs and 258 lbs). The resultant bending force applied to the shaft is 1221 lbs. at an angle of 8.2° as shown.
Now assume that Ground Idle Power is 35 HP (enough to spin the both rotors at no-load, plus the accessories), which is 43 lb-ft of torque at 4250 RPM. That produces a driving tension in the belts of 166 lbs. The driving tension becomes the difference between the tight and loose spans. The preload is 1226 lbs, determined above, so the tight side tension is 696 lbs. and the loose side tension is 530 lbs. The resultant of those two forces is 1219 lbs. at an angle of 5.5°, as shown in the sketch below. The slight difference is due to the small change in direction of the resultant of the two vectors.
That demonstrates the fact that when the transmitted power is reduced, the net bending force applied to the shaft remains the same.
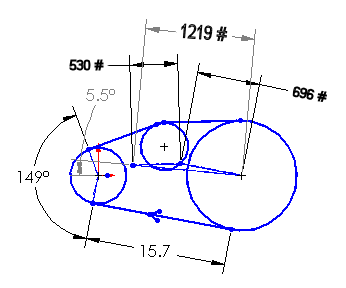
V-belt Drive at Idle Power
EFFECTIVE TORSIONAL RATE
Belts (and chains and pretty much everything else) stretch when a tension force is applied to them. Imagine that the driven pulley is fixed and cannot rotate. When a torque is applied to the driving pulley, the belt stretch allows that pulley to rotate slightly. That rotation, caused by the belt stretch, introduces an additional torsional spring rate into the system. The effective torsional rate of the belt drive is the applied torque divided by the angular deflection of the driving pulley caused by the belt stretch.
Using a typical modulus for a 3V-section belt, the torsional rate of the main belt system works out to approximately 200 lb-ft per degree.
It is fortunate, indeed, that the stretch modulus for V-belts is relatively low (they are springy). That property is what cushions the engine spikes significantly. When positive engine torque spike occurs, the belts stretch. When the engine torque goes negative, the tight-side momentarily becomes the "loose" side because the tensile force in the "tight" side has been reduced below preload. That allows the centrifugal component of the belt load to push the entire "tight" side span outward, resulting in the wild "flapping" observed in that system.
