Technical Articles and Product Descriptions

Reference Materials

Additional Products

Race Engine Technology Magazine

Figure 1 shows the torsional excitation generated by an even-fire 8-cylinder engine (explained in ENGINE TORSIONAL EXCITATION). This is a "fourth order" excitation, which at an 800 RPM idle, produces 53 pulses per second (Hz), and at 5000 RPM, produces 333 pulses per second (Hz). Note that the four torque peaks are nearly twice as high as the mean torque produced by the engine (the torque measured by the dynamometer).

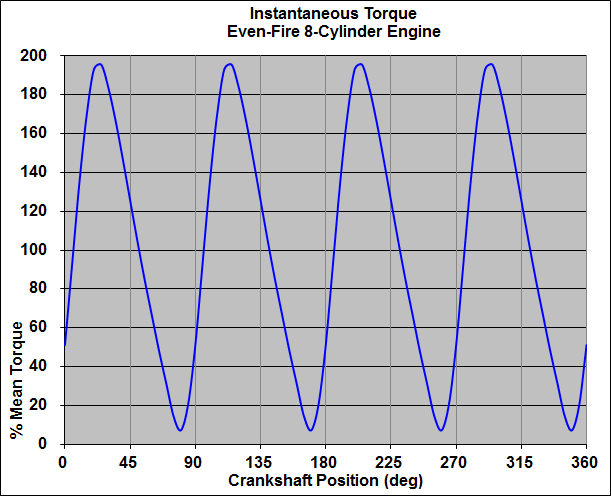
FIGURE 1

One might think it would be sufficient to design a PSRU to sustain the loads produced by the input torque peaks. However, depending on the resonant frequencies of the engine-PSRU-propeller system, the PSRU and the propeller can be subjected to vibratory forces many times HIGHER than the peaks produced by the engine. The following discussion explains how that can happen. (The fundamentals of vibration are presented in Vibration Basics and Torsional Vibration Overview.)

The ratio between the amplitude of the excitation torque (the size of the pulses) and the amplitude of the output torque is expressed by a value called transmissibility. For the Engine-PSRU-Prop system, the engine torque variation (as shown in Figure 1) multiplied by the transmissibility equals the torque variation applied to the PSRU, which is then multiplied by the gear ratio and applied to the prop.

Figure 2 shows how transmissibility changes with excitation frequency and with damping. The horizontal axis is frequency ratio (r), which is the excitation frequency divided by the resonant frequency. The symbol "β" shows the amount of damping in the system. β=0 is none, β=2 is a lot.

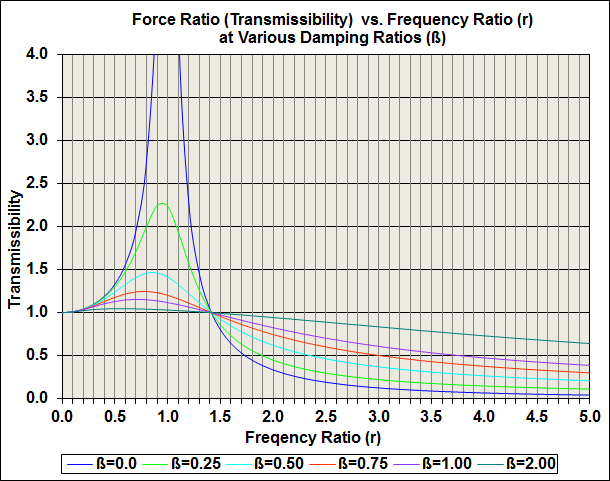
FIGURE 2

The different curves in Figure 2 show how transmissibility will change as the excitation frequency changes from zero to five times the resonant frequency (frequency ratios {r} from 0 to 5), and with different amounts of damping (β) . Note that at r=1 (resonance) the system with no damping (β=0) allows the transmissibility to become huge (theoretically infinite).

The solution for the resonant frequency can be done several different ways. We have written a program that uses the Ho9lzer

Notice that all the curves in Figure 2 have the same transmissibility at r = 0 (which is completely obvious) and at   r = 1.414 (which is √2 and is easily proven with the governing equation). The point at which all the curves go from amplification (T > 1) to suppression (T < 1) is called the crossover point.

Note that below crossover, the more damping the system has, the less the input waveform will be amplified, but AMPLIFIED IT WILL STILL BE. Understand this: No matter how much damping is added, if the engine-PRSU-Propeller system is operating below crossover, the PSRU (thus the gears, shafts and propeller) feels torque pulses GREATER than what the engine produces. If operation below crossover is unavoidable, then adding damping significantly reduces the amplification around resonance. However, it is very important to notice that as you add DAMPING to the system, the pulse suppression which is available above crossover is dramatically reduced. Then, if you really need the band-aid of damping, it can be problem to implement that damping in a reliable manner, and to cool it. Remember: dampers convert motion energy to heat energy.

For anyone interested, the following is the equation for transmissibility, using the parameters defined above:

Clearly, to solve that equation, you must have first determined the resonant frequency of the system you are analyzing. That subject is covered in detail HERE.

The following example shows the practical implications of transmissibility in a PSRU system. Figure 3 shows the transmissibility curves of two different PSRU systems for the same V-8 engine and propeller. The first-mode resonant frequency for one system (red line) is at 450 RPM; the other (blue line) is at 3700 RPM.

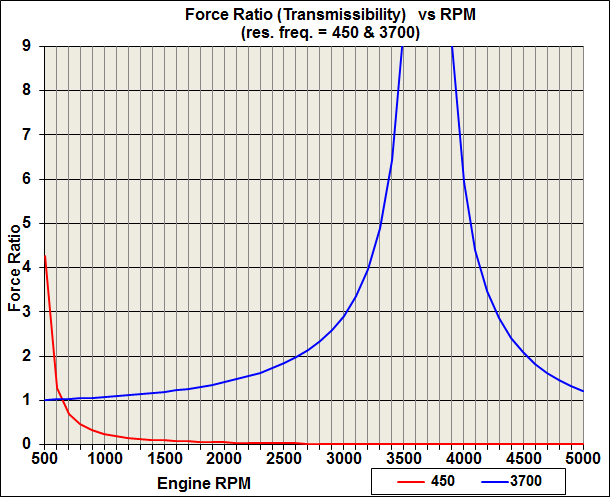
FIGURE 3

In order to examine the effect those different resonance points have on gear and propeller loads, let's determine the torque variation seen by the PSRU in each system while being driven at 4000 RPM by an engine such as the one shown in Figure 1 (625 lb.-ft. mean torque, with peaks of 1235 lb.-ft. and valleys of 68 lb.-ft.).

First, consider the system with the resonant frequency at 3700 RPM. At 4000 RPM, the transmissibility is 5.93, which means the engine torque pulses (from 68 to 1235 lb-ft) are amplified nearly 6 times before reaching the PSRU, and range from valleys of -2678 lb-ft. to peaks of +4243 lb-ft. It is easy to see why this gearbox and prop did not last very long.

Now consider the system with the resonant frequency at 450 RPM. At 4000 RPM, the transmissibility is .013. That means the engine torque pulses (which range from 68 to 1235 lb-ft) are nearly erased. The torque which is applied to the PRSU varies from a low of 618 to a peak of  633 lb-ft. This is "turbine-smooth".

In order to design and evaluate Engine-PSRU-Propeller systems, EPI has implemented several useful computer programs which assist us in the design of our very effective Engine-to-Gearbox coupling system, that can provide transmissibility numbers below 0.10 in the normal operating ranges (nearer to 0.010 at cruise and takeoff power settings).

This coupling system takes into account the properties of the whole powerplant (engine, gearbox, reduction ratio, propeller characteristics) in order enable the designer to locate the system-first-mode resonant frequency well below engine idle speed.

One of the most useful programs in that suite is one which calculates, with great accuracy, the effective engine MMOI values from data which include the crankshaft stroke and weight, number of journals, bobweight value, and the dimensions of the flywheel, torsional absorber, and accessories. That program uses known measured values from the industry as a validity cross-check, and the methodology is commonly known.