- Torsional Vibration Overview -
This subject is especially interesting with respect to piston engines
and the stuff they drive
NOTE: All our Products, Designs, and Services are SUSTAINABLE, ORGANIC, GLUTEN-FREE, CONTAIN NO GMO's, and will not upset anyone's precious FEELINGS or delicate SENSIBILITIES.
Consider the system represented schematically in Figure 1. It consists of a heavy flywheel, rigidly mounted on a round shaft. The shaft is supported in a frictionless bearing at the flywheel end, and rigidly attached to a big strong wall at the opposite end.
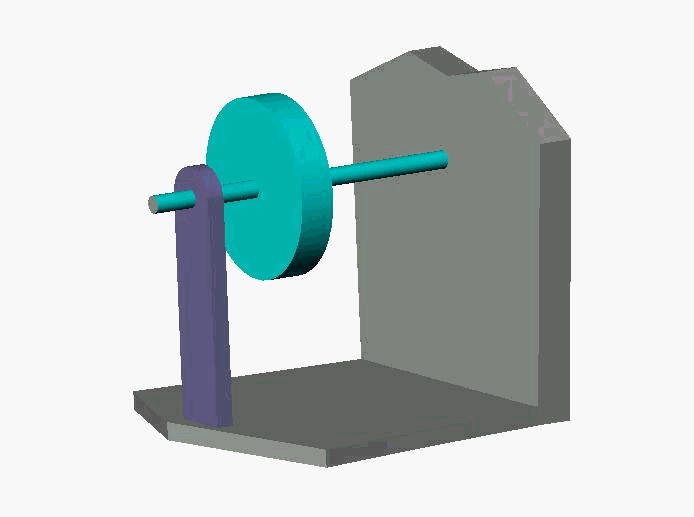
FIGURE 1
Single Degree of Freedom Torsional System
Suppose you grabbed the rim of the flywheel with both hands and twisted it like a steering wheel. The wheel turns a bit, but the rotation of the wheel is resisted by the twisting action of the shaft. When shaft has twisted enough to exert the same resisting torque on the center of the wheel as you are applying to the rim, the wheel turns no further. As you slowly relax your twisting force, the wheel returns to its neutral (untwisted) position.
The shaft (if it has not been twisted excessively) has acted like a particular kind of spring known as a torsion spring or torsion bar. The torsional spring rate of the shaft can be defined as the amount of torque it takes to twist it one degree (symbolized by "Kt"). The torsional rate can be calculated if the dimensions and material of the shaft are known.
Now suppose you twist the wheel again, but instead of releasing it slowly, you suddenly let go. What happens? The energy stored in the shaft (torsion spring) exerts a torque on the flywheel, which accelerates the flywheel toward its neutral position. When the flywheel reaches the neutral position, the flywheel has reached its maximum velocity. The shaft has released all its stored energy, and the flywheel has recovered that energy (which had been stored in the spring) and has stored it as kinetic (motion) energy.
Because the flywheel is in motion, it continues to rotate past neutral. After the flywheel passes the neutral position, the shaft begins to deflect again, opposing the motion of the flywheel, and begins to decelerate it. When the resistance of the shaft stops the flywheel, it has rotated (theoretically) to the same angular distance past neutral as when you released it, but in the opposite direction. The shaft has recovered the wheel’s kinetic energy and converted it (again) to deflection energy. The shaft now begins to accelerate the wheel back in the other direction.
This back-and-forth motion of the flywheel and shaft is an example of torsional vibration. In an idealized world, this vibration goes on forever. In the real world, there is always some energy lost, so the vibration eventually stops (there are no practical frictionless bearings, and springs have some amount of hysteresis loss, and everyone knows about aerodynamic drag).
In this example, we are interested in how many times per second (how frequently) the wheel oscillates (cycles) back and forth. That frequency is the resonant frequency of the torsional system. The value of the resonant frequency can be calculated if you know two values: (1) the torsional rate of the shaft (Kt) and (2) the mass moment of inertia (MMOI) of the flywheel (symbolized "Jm").
The MMOI of a flywheel is a calculated value, related to it's weight, which takes into account how far the weight is concentrated from the center of rotation. The MMOI is a measure of how difficult it is to accelerate or decelerate the flywheel, and can be thought of as "FLYWHEEL EFFECT".
Now suppose the Jm and the Kt of the system pictured in Figure 1 are such that the resonant frequency is one cycle per second (1.0 HZ). Also suppose that the we get a Very Coordinated Person to apply a 10 LB. yank on the flywheel rim, in the direction the wheel is starting to move, every time it changes direction (every half-second). The input from the VCP has changed the system into what is known as a Forced Vibration System. The 10-LB. yank every half-second is called a driving force, or an excitation force.
Now what will happen to the system? Because it is being driven at its resonant frequency and is essentially without damping, the number of degrees the flywheel moves will increase with every oscillation until the weakest part of the system (perhaps the shaft, perhaps the attachment of the shaft to the wall, perhaps the attachment of the flywheel to the shaft) fails. This situation is an example of undamped, forced vibration at resonance. It is a system which is out of control.
The study of forced vibration systems shows that when the excitation force is sinusoidal (in the shape of a sine wave) and is periodic (repeats itself over and over), then the system will vibrate at the frequency of the excitation.

