Technical Articles and Product Descriptions

Reference Materials

Additional Products

Race Engine Technology Magazine

This section describes the general properties of V-belt and Toothbelt transmission systems, and provides a detailed explanation of PRELOAD, a necessary component of all types of belt drives.

BELT DRIVE BASICS

In order for a belt drive to operate properly, the residual tension in the "loose" span (the non-driving span) of the belt can never be allowed to get near zero (unlike a chain drive, where the "loose" span can actually be loose.). That requirement is accomplished by establishing a static "preload" on the belt. The term "preload" means the establishment of a static tension value in all the spans of the belt.

For V-belt drives, preload maintains the contact force between the belt and the surface of the pulley grooves so that friction can transmit the power. For toothbelt drives, preload maintains the correct contact pattern between the belt teeth and sprocket grooves. The preload for V-belt drives is usually greater than that required for toothbelt drives.

Any belt will stretch when a load is applied to it, although the amount of stretch is usually very small. The amount of force to produce a specified stretch is k nown as the belt modulus.

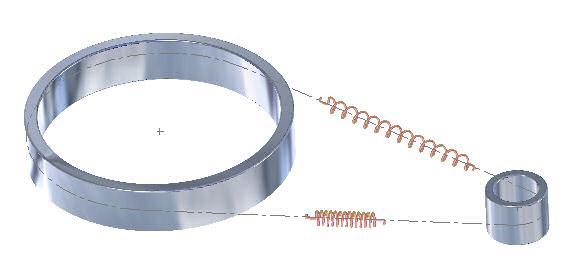
The static preload (system not running) in the system stretches each span (spring) of the belt equally, as illustrated in the picture below.

The amount of preload required in a belt drive depends on a number of factors, including:

1. the maximum amount of torque which the drive must transmit;
2. the diameter of the driving sprocket (pulley);
3. the minimum arc of contact between the belt and sprockets ("wrap");
4. the properties of the belt.

Preload can be established by means of adjusting the centerline distance between shafts (shimming) or by using an idler which imposes a side load on the "loose" span.

Everyone is probably familiar with establishing preload on an automotive fan-belt system by wedging on the pivoting alternator and locking it in place with the slotted locator arm. With more modern vehicles, the preload (on a serpentine system) is established by a spring-loaded idler in the last span of "slack".

You are also probably familiar with the result of not having enough preload in the drive: the belt will slip and squeal under high load. That happens frequently with power steering belts when you turn the steering wheel up against one of the stops.

When torque is applied to the driving sprocket (pulley) of a belt drive, one span of the belt gets tighter and stretches slightly in response to the additional load applied by the driving torque. At the same time, the load in the loose span reduces by the same amount, and the loose span shortens by the same amount the tight side stretched.

Clearly then, the tension in the tight (driving) span becomes greater than the preload, and conversely, the tension in the loose span becomes less than the preload. This behavior is illustrated in the picture below.

When a belt drive is operating and transmitting power, the amount of force being transmitted from the driving sprocket (pulley) to the driven sprocket (pulley) is the difference between the tension in the " tight" (driving) span of the belt and the tension in the "loose" (following) span of the belt.

NOTE that the sum of the tight and loose strand tensions is always the same, which means that the bearing loads and shaft bending load caused by a belt drive will be essentially constant, regardless of the torque being transmitted. (Only the angle of application changes with applied torque).

The value of the tension in the tight (driving) span is the sum of two values: (a) the "driving tension" plus (b) the existing "loose-side" tension, as shown above. The "driving tension" is the tension in the tight span produced by the torque applied to the driving sprocket (pulley), and has the value:

Driving Tension = applied drive torque / drive sprocket pitch radius

For example, a torque of 2760 lb-in (230 lb-ft) applied to a sprocket of 2.155 pitch radius (4.311 pitch diameter) produces a driving tension of 1281 pounds (2760 / 2.155). If a smaller diameter driving sprocket is used, say 1.705 pitch radius (3.409 pitch diameter) then the driving tension increases to 1620 pounds (2760 / 1.705).

The amount of preload which a belt drive requires is specified by a value known as "tension ratio" (TR), which is expressed as:

TR = Tight-Side Tension / Loose-Side Tension

Knowing that Tight-Side Tension is the sum of the Driving Tension plus the Loose-Side Tension, that equation can be rewritten as:

TR = (drive tension + loose-side tension) / loose-side tension

or (by means of some high-school algebra)

TR = 1 + (drive tension / loose-side tension)

Rearranging that equation produces the more useful form:

Loose-side tension = Drive-tension / (TR - 1)

The value of the preload can be approximately measured by applying a side force to one span and measuring the force required to deflect the belt a specified amount. Note that the side-load checking force you apply at midspan is NOT THE PRELOAD. The mid-span side force required to produce the specified deflection just a rough measure of the belt preload.

The force and deflection values used to measure preload are a function of the "springiness" of the belt and the length of the span, and can be calculated from data provided by belt manufacturers.

V-BELT DRIVES

The transmission of force from a pulley to a V-belt (and the inverse) depends on friction between the belt and the pulley. The friction force between the belt and the pulley depends on three factors:

1. the normal force between the belt and the pulley (that is, the force which is perpendicular to the side surface of the groove),
2. the coefficient of friction between the belt and the pulley, and 
3. the arc of contact between the belt and the pulley.

You already know (explained in Force and Friction) that the frictional force between two objects is the product of the coefficient of friction and the normal force. The coefficient of friction is independent of the shape of the belt, but the normal force between the belt and sides of the pulley sheave depends on:

1. the included angle between the sheave sides, and
2. the tension on the belt.

Because of the wedging action between the belt and the pulley, the normal force is a significant multiple of the belt tension.

In order for the system to transmit the required torque, the belt(s) must be wedged into the groove(s) tightly enough to transmit the applied force.

In order to achieve the necessary wedging, it is necessary to apply a static preload to the drive system. The required preload is calculated from three factors:

1. the maximum torque to be transmitted by the drive,
2. the minimum arc of contact, and
3. the pitchline velocity of the belt(s) (to account for the effect of centrifugal force, which reduces the wedging effect).

Belt manufacturers recommend that the tension ratio for a system with 180° of contact on each sheave should be no tighter than 5:1 (when a new belt has been installed) and no looser than 8:1 (after the belt has run-in).

If the arc of contact on any load-transmitting pulley in the system is less than 180°, then the required tension ratio decreases, which means more preload.

TOOTH-BELT DRIVES

Preload in a toothed-belt system is required in order to keep the teeth from attempting to climb up the sides of the grooves in the sprockets, and, in extreme cases, from jumping ("ratcheting") under the most severe loading conditions.

In a static (non-moving) toothed-belt drive, the tension force in each span of the belt is equal, and is determined by the required preload. The required preload is determined by four factors:

1. the recommended tension ratio.
2. the number of teeth engaged on the driving sprocket,
3. the pitch diameter of the driving sprocket,
4. the maximum torque to be transmitted by the drive, and

If the preload of a toothbelt is slightly less than required, the teeth will try to climb the sides of the grooves at high torque loadings, which leads to (a) rapid wear of the belt, and (b) very high shaft bending loads (higher than if the preload were correct).

Belt manufacturers recommend that the tension ratio for a system with more than a defined minimum number of teeth in contact on the smallest sprocket should be in the range of 8:1 to 10:1 (after the belt has run-in).

There are rumors, claims, counterclaims and just plain false information floating around regarding the use of the Gates Polychain™ Toothbelt as a propeller reduction transmission method. I think it is important to debunk the myths and rumors and put some numbers to the claims. The issues covered here are:

1. Belt Preload,
2. Belt Stretch Under Load,
3. Belts Breaking in Service,
4. Change in Preload with Temperature,
5. "Mah Harley don't need no Preload" ,

1.  PRELOAD:

Our contact in Gates engineering is one of the people responsible for the PolyChain engineering manual. In July of 2004, he told us that Gates is in the process of updating their manual to reflect some of the new engineering data they have gathered from field experience with the PolyChain toothbelt. One of the important changes is the fact that the maximum recommended tension ratio is being increased from 8:1 to 10:1 (That means the minimum allowable preload is LESS than before. (If you don't understand tension ratio, check it out here.) Throughout the EPI website, the calculations for loads imposed by the PolyChain toothbelt drive have been updated to reflect this new information.

The text below is a direct copy of the information in the Gates Manual with respect to the self-tensioning which results from insufficient preload in a PolyChain drive system:

Gates PolyChain GT2 Design Manual, Page 110:

"All synchronous belt drives exhibit a self-tightening property when transmitting a load. Lab testing has shown this property is similar for all tooth profiles. The designer should be aware that self-tensioning can result in increased bearing and shaft loads, as well as reduced belt life. These effects can be AVOIDED by following proper tensioning procedures."

"Belt overtensioning can impose unnecessarily high bearing and shaft loads. However, belt undertensioning results in self-tensioning. When a belt is too loose for the design load, the belt teeth try to climb the sides of the sprocket grooves, which dramatically increases the stresses on the belt, the belt teeth and the shafts and bearings, leading to rapid tooth wear and reduced component life."

Here is an example from a low-powered helicopter application: - - In order to transmit 95 HP at 2168 RPM (230 lb-ft of torque) to the main rotor, using a 34-tooth drive sprocket, a 144-tooth driven sprocket with a 20.5 inch centerline distance, with an 8mm pitch, 62mm wide PolyChain GT2™ belt, the Gates analysis program (as well as the EPI program, which we wrote using the calculations provided in the Gates Engineering Manual) show that, on a used belt (more than about 10 hours on it), in order to achieve the correct PRELOAD to that system, there should be a DEFLECTION of 5/16" at mid-span from a SIDE LOAD of 53 to 60 pounds. Note that to get the right PRELOAD for 120 HP in that same system, the side load to achieve the specified mid-span deflection for a used belt should be 72 to 78 pounds.

(Be sure you understand the difference between PRELOAD and SIDE LOAD.)

The distinction between new and used belts is necessary because in the first few hours of operation of a new belt, the belt takes a small permanent stretch, which has the effect of reducing the preload. So the preload values for a new belt are higher than for a used belt, in order that the correct preload remains after the new belt stretches.

2.  BELT STRETCH:

From that same low-powered helicopter example, in order to transmit 95 HP (230 lb-ft of torque at 2168 RPM) to the main rotor, using a 34-tooth drive sprocket and an 8mm pitch, 62mm wide belt, the driving tension load (that is, differential tension, not including preload) in the belt is about 1620 pounds (aplied torque x driving sprocket pitch radius).

Gates Engineering has provided EPI with the belt modulus which they use to calculate the stretch of a PolyChain belt in response to a given load. Using the Gates methodology and that modulus, we calculated the belt stretch produced by (a) 1620 pounds of tension applied to (b) an 8mm Pitch, 62mm wide PolyChain GT-2 belt over a tensile span of (c) 19.75 inches. That stretch is 0.066 inches (just a hair over 1/16 of an inch), and is in addition to the static stretch caused by the preload.

That stretch value (0.066") agrees exactly with the value which Gates Engineering calculates for the same boundary conditions.

That stretch value provides some insight into why preload is required to prevent tooth climbing and skipping under load.

3.  BROKEN BELTS:

I have dealt with several cases of Gates Polychain belts fracturing across a single tooth root. The belt shown in this picture broke after slightly more than 3 hours of operation.

Figure 1

EPI sent that (pictured) broken belt to Gates Engineering for analysis. Their opinion (a consensus of several knowledgeable Gates engineers) is that the belt almost certainly fractured because of being operated in an undertensioned drive system. They said there was clear evidence of the belt having skipped teeth, which severely overstresses the belt cords AND the shafts AND the bearings.

A copy of that report from Gates is shown in Figure 2 below. (It has been edited to remove names and phone numbers. REMEMBER, Gates doesn't want their stuff on aircraft.)

Figure 2

4. PRELOAD CHANGES WITH TEMPERATURE:

Some designers and PSRU purveyors claim temperature change does not significantly alter the loading in the system. Part of the convoluted reasoning behind that claim is based on their incorrect grasp of belt stretch (explained above).

If you think we're making this up, go check the belt tension on YOUR system when the aircraft has sat overnight and is at ambient temperature, and then go out and fly for a half hour, and check the tension again. You will find that the belt has tightened substantially by warming up (and it will have relaxed somewhat from the cooling effect of descent and landing).

Our calculations (using moduli and methodology provided by Gates Engineering) show that, for a 50°F rise, the helicopter system we mentioned above gains almost 400 pounds of preload.

That increase comes from 3 sources:

1. 150 lbs. from shrinkage of the belt,
2. 220 pounds from growth of the 144-tooth output aluminum sprocket,
3. 21 pounds from growth of the 34-tooth iron sprocket..

The total rate of tension increase from the specifics of the system described in a, b, and c above is about 7.8 pounds per degree F. AND that does NOT include the expansion / contraction of the PSRU housing.

In fact, that points out a major problem with the a fixed-center, no-preload-pulley system, that no matter how carefully you adjust the center distance, YOU CAN NEVER KNOW WHAT THE REAL PRELOAD IN THE SYSTEM IS AT ANY POINT IN TIME, because it changes significantly with the temperature of the components.

5. "MAH HARLEY DON'T NEED NO PRELOAD"

That argument has been presented to me several times to support a claim that somehow, their belt drive is somehow immune from the need for preload.

Let's look at the differences between "Mah Harley" and the belt system likely to be used for a propeller reduction unit.

First, the power level being transmitted by the Harley belt drive is extremely low about 95% of the time. How low, you ask?

Well, it's fairly easy to figure out. One of my friends has a belt-drive Harley, and he has taken careful data which shows he gets 46 miles per gallon at a steady 70 MPH (freeway). That is a fuel consumption of 1.52 gallons per hour, or about 8.9 pounds per hour. If we use a conservative estimate of 0.48 for the BSFC of the old 45° V-twin, then the power the engine produces to cruise at 70 is 18.5 HP (8.9 pph / 0.48 = 18.5 ).

The outside diameter of the rear wheel of his bike is about 26 inches, so at 70 MPH, the rear wheel is turning 775 RPM. Assume that only 1/2 HP is lost between the crankshaft and the rear wheel, so that 18 HP is going on the road. 18 HP at 775 RPM requires a torque of 122 lb-ft. The belt sprocket on the rear wheel is about 10" in diameter, so the belt driving force to transmit 122 lb-ft is about 293 pounds.

Consequently, the preload Harley specifies for their belt is quite a bit less than what is needed on the helicopter main rotor drive. In fact, at a 10:1 tension ratio, 293 pounds of driving tension requires only a 32-pound preload.

Second, the preload Harley specifies (recommended by Gates, since they developed the belt specially for HD) is the value based on the cruise load, since that is the predominant loading the machinery sees.

Third, the tooth and sprocket profiles Harley uses were developed by Gates for the specific purpose of being able to tolerate the occasional burst of wide-open throttle without needing to have the preload set for the high-power operation. It's not the same tooth profile as you have in your PSRU or helicopter.