Technical Articles and Product Descriptions

Reference Materials

Additional Products

Race Engine Technology Magazine

A "combustion engine" is a device which converts the chemical energy stored in a fuel into heat energy, and then converts a portion of that heat energy into mechanical work. Any combustion engine can be effectively visualized using what is commonly known as the "Black Box" model. (A "Black Box" is a colloquial name for a conceptual entity which has known inputs and outputs, and which performs a defined function, but whose innards and functioning are unknown.)

The following is a sketch of the "black box" which represents a combustion engine.

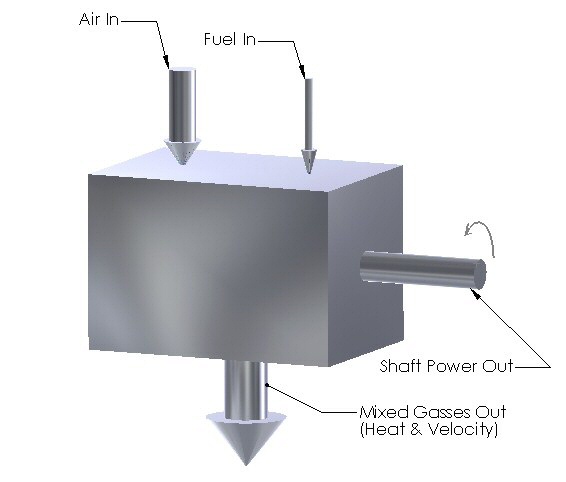
The sketch is fairly self-explanatory. Air and fuel go into the box. Something happens inside. Shaft power comes out, along with an eclectic mixture of waste gasses, which contain both heat and velocity. (Acoustic energy and other small losses have been ignored here for the sake of simplicity.)

That model applies equally well to piston and turbine engines. In the turbine case, there is relatively more velocity in the exhaust stream, and there might or might not be any external shaft power extracted (turboshaft vs. turbojet). In both turbine and piston engines, the output gasses include heated air (from heat exchangers and air not consumed by combustion) and very hot gasses which are the products of combustion.

The exit configuration will define the temperature, pressure and velocity of the exiting stream. In certain applications, the exiting stream is a mixture of both components (cooling and exhaust gasses) and can be used to generate thrust.

The energy source for an engine is the chemical energy stored in the fuel. That energy is released by the oxidization of the fuel (combustion) by an oxidizing medium, which in most cases is the oxygen which makes up about 20.95% (by volume) of the air we breathe. Variations on that theme include the use of oxidizing additives (Nitrous Oxide, for example) and high-energy fuels which contain a substantial supply of oxidizer in their makeup (Nitromethane, for example).

For this explanation, assume we are discussing a piston engine operating on gasoline for fuel. (This analysis works for Gasoline, Methanol, Diesel fuel, Jet fuel, Whale Oil, Whatever. Each fuel has it's own weight and energy content.)

Gasoline, according to Pratt & Whitney Aircraft data sheets, has a specific gravity of 0.71, and therefore a weight of about 5.92 pounds per gallon, and releases approximately 19,000 BTU of energy per pound of fuel burned, known ad the Lower Heating Value.

What is a BTU? A "British Thermal Unit" is defined as the heat energy required to raise the temperature of one pound of pure water by one degree F, and is equivalent to 778 foot-pounds of work / energy. By arithmetic, it can be shown that one horsepower (33,000 ft-lbs per minute) is the equivalent of 42.4 BTU's per minute or 2545 BTU's per hour, calculated as follows:

How is that useful?  Here is an example. We have tested a reasonably good 4-stroke piston engine which converts approximately 24 gallons of gasoline per hour ( 142 pounds of fuel per hour ) into 300 measured horsepower.

So how much of the total fuel energy does this engine convert into horsepower? If you burn 24 gallons of gasoline (142 pounds) over the course of one hour, you release 2,699,520 BTU's of energy (19,000 x 142). If you divide the 2,699,520 BTU's by 2545 (the number of BTU's-per-hour in one HP), you discover, to your surprise, that it is 1061 HP. But the engine is only making 300 HP. Where is all the rest of that energy going?

It is a known fact that a piston engine does a rather inefficient job of converting fuel energy into power. The rule of thumb approximation is that nearly 1/3 of the fuel energy goes out the exhaust pipe as lost heat, approximately 1/3 of the fuel energy is lost to the cooling system (coolant, oil and surrounding airflow), leaving roughly 1/3 of the energy (best case) available for power output. Some of that power is lost to making the pistons go up and down, driving accessories (oil pump, coolant pump, alternator, vacuum pump, hydraulic pump, etc.), losses from pumping air through the engine, thrashing the oil in the crankcase, and friction in various forms.

The difference between the energy content of the fuel consumed and the useful power extracted from the engine is known as Thermal Efficiency (TE).  So in our 300-HP engine example, the TE is 300 HP / 1061 HP = 28.3 % (which is fairly good by contemporary standards for 4-stroke production piston engines).

The calculation for Thermal Efficiency (TE) is:

Equation 1

Going back to our 300 HP example, TE =  0.1339 x 300 HP /  142 PPH = 0.283 (28.3 %)

(Note that when using % in a calculation, you must divide the percentage number by 100. That is how 28.3 % becomes 0.283.)

If you prefer gallons per hour, the Thermal Efficiency calculation is:

The value of this Thermal Efficiency relationship is that, by assuming a reasonable TE value (27% - 29%), you can estimate the amount of fuel required to produce a given amount of power.

Suppose, for example, that you need to produce 300 HP. What will be the required fuel flow assuming 28.3% TE ?

Brake Specific Fuel Consumption (BSFC)

A more commonly used yardstick for expressing thermal efficiency is known as Brake Specific Fuel Consumption (BSFC). It is simply fuel flow (in pounds-per-hour) divided by measured HP, and is expressed in Pounds-per-Hour-per-HP.

Equation 2

This tool is also an important yardstick for comparing the performance of one engine to another and for evaluating the reasonableness of performance claims.

An excellent BSFC for a well-developed, 4-stroke naturally-aspirated, high-performance liquid-cooled engine at 100% power is in the neighborhood of 0.44 – 0.45. Claims of gasoline engine BSFC values less than 0.42 at max power tend to be suspect. At reduced power settings (in the region of 70% and below) BSFC values of 0.38 have been achieved, and will become more commonplace as refinements of combustion technology evolve in the pursuit of energy conservation.

The operator manual for a 300 HP Lycoming IO-540-K, L, or M series engine shows a full power fuel flow of 24 GPH which is a BSFC of 0.474 ( 24 * 5.92 ÷ 300 ) and a TE of 28.3% (explained above). Those numbers aren't too bad for an air cooled engine which meets the FAR-required detonation margins. However, the turbocharged TIO-540-V2AD requires a MINIMUM of 39.2 GPH at 350 HP for a BSFC of 0.663 and a TE of 20.4%.

So if someone tells you that they have developed a 4-stroke piston engine which, at max power, makes 300 HP on 20 GPH of gasoline, you can quickly calculate a BSFC of 0.39 and a Thermal Efficiency of 34.4%. You should be highly suspicious of such a claim.

There are many documented examples of well-developed engines producing maximum power at BSFC figures in the 0.45-0.48 range. If we use an estimated BSFC as a starting point, it is straightforward to calculate the airflow the engine will require to produce a specified HP.

We know that air density is 0.0765 lb / cubic ft at sea-level-standard conditions of 14.7 psia (101.325 kPa) and 59°F (15°C). We also know that a pound of gasoline releases about 19,000 BTU when burned, and that the typical best-power air / fuel ratio is between 12.6 and 12.9 lb / lb.

So with that knowledge, if we needt to estimate the airflow required from an engine to develop a given amount of power, that can be calculated with an assumed BSFC and best-power AFR.

So, for example, if we estimate BSFC at 0.47 lb / HP / hour and best-power AFR of 12.6 (quite reasonable numbers), the required airflow is for 600 HP is::

Then the question becomes: how fast do you want to run the engine to produce that airflow? That is answered in the next section, titled Volumetric Efficiency.